初探RSA算法

Created2023-01-09Updated2023-04-25Visited

RSA简介

RSA加密算法是非对称加密算法中的一种，在1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的，并取三人名字的首字母命名该算法。
RSA加密算法因其可靠的安全性（目前看来是十分安全的），得到了广泛的认可和使用，ISO（国际标准化组织）、ITU（国际电信联盟）及SWIFT（环球同业银行金融电讯协会）等国际标准组织均采用RSA作为加密标准，PGP等协议也采用RSA算法来传输会话密钥和数字签名；
RSA算法的主要核心在于欧拉定理

数论知识

一、质数的定义：在一个大于1的自然数中，如果只有1和它本身两个因数，那么这样的数叫做质数或者素数

二、互质的定义：在两个正整数中，除了1之外没有其他的公因子的话，我们便称这两个数为互质关系
关于互质的推论：
(1)1与任何数互质
(2)两个质数互质
(3)当两个数中，大数为质数的话，两个数互质
(4)在两个数中，一个数为质数，另一个数不为其倍数；则这两个数互质
(5)当p为正整数时，p与p-1互质
(6)当p为奇数时，p与p-2互质

三、同余定理：对于给定的一个正整数m，若是对于两个整数a、b来说；a-b能被m整除的话；则称a与b对于模m同余；
记作a ≡ b ( mod m)

四、欧拉函数:我们主要利用欧拉函数来计算在1到n内有多少个数与n为互质关系；这里我们用φ(n)来表达这个值
(1)当n=1时；φ(n)=1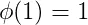

(2)当n为质数时，φ(n)=n-1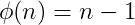

(3)当n=p^k(p为质数，k为指数，n为p的k次方)；φ(p^k)=p^k-p^k-1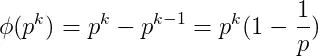

(4)当n为两个互质的数的积时，φ(n)=φ(pq)=φ(p)φ(p)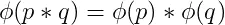

(5)当n为任意大于1的正整数时，φ(n)=φ(p1^k1 * p2^k2 * p3^k3…pn^kn)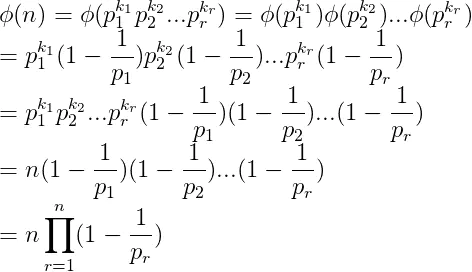

五、欧拉定理：对于两个互质的数p、q;可得p^φ(q)≡1mod(q);也可以写成p^φ(q) mod(q)=1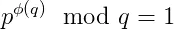

六、费马小定理：费马小定理是针对欧拉定理的特殊情况，是当q为素数的时候；φ(q)=q-1；
所以上式又可以写成p^(q-1) mod(q)=1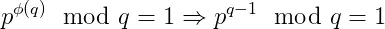

七、模反元素的定义，当p与q互质时一定会存在一个数b使得p * b≡1mod(q)也可以写成p * b mod(q)=1；证明过程可以依据欧
拉定理的变形p^φ(q) mod(q)=1=p * p^[φ(q)-1] mod(q)；此时称b为p的模反元素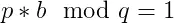

非对称性加密的信息传递过程

B将公钥(i,n)传递给A
A拿着公钥(i,n)对明文使用公钥加密算法对明文进行加密
A将密文传递给B
B拿着私钥(j,n)对密文进行私钥解密算法对密文进行解密
在这个过程中i、n为公开的，只有j为私密的；当j被攻破时，也就证明者加密的内容可以被攻破

密钥的生成

1.选择两个互质的数p、q(实际中两个质数越大就越难破解，因为逆向计算过程非常的不容易)
2.计算p与q的乘积n(n的长度就是密钥长度。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。)
3.计算n的欧拉函数φ(n)
4.随机选择一个数e，条件是e与φ(n)互质，且e的范围在(1,φ(n))之间
5.计算e对于φ(n)的模反元素d；即ed mod(φ(n))=1;即为ed-1可以被φ(n)整除
6.此时将n、e封装成公钥，n、d封装成私钥；此时的公钥即为(n,e) 私钥为(n,d)
注：实际应用中，公钥和私钥的数据都采用ASN.1格式表达（实例）

RSA算法的可靠性

回顾上面密钥的生成一共出现了p、q(两个互质的数)；n(p、q的乘积)；φ(n)(n的欧拉函数)；e(与φ(n)，且范围在(1,φ(n)))
;d(e对于φ(n)的模反元素)；这六个数字之中，公钥用到了两个（n和e），其余四个数字都是不公开的。其中最关键的是d，因为n和d组成了私钥，一旦d泄漏，就等于私钥泄漏。
破解：那么在我们已知n和e的情况下，有没有办法破解出d呢？
此时我们进行逆推，d是怎么算出来的呢?d是e对于φ(n)的模反元素即ed-1可以被φ(n)整除；那么此时的计算式为ed modφ(n)=1
所以此时我们需要知道e和φ(n)；
那么e又是怎么来的呢?e是一个与φ(n)互质的数且范围在(1,φ(n))内；所以我们就需要知道φ(n)
那么φ(n)又是怎么来的呢?
φ(n)来源于两个互质的数p、q的乘积的欧拉函数
所以综上所述，只有将φ(n)分解成两个互质的数的乘积，才可以算出私钥；所以RSA的破解在于大整数的因数分解；目前，除了暴力破解，还没有发现别的有效方法。
维基百科这样写道：

1
2
3
　"对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。
　　假如有人找到一种快速因数分解的算法，那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。
　　只要密钥长度足够长，用RSA加密的信息实际上是不能被解破的。"

加密

加密分为两个步骤，求幂和取余；首先我们需要知道公钥(n,e)此时我们假设明文为m，密文为c
首先求幂m^e;然后取余(m^e)%n;此时(m^e)%n就是我们的密文;用式子表达就是　m^e ≡ c (mod n)

解密

解密仍然是分为两个步骤，求幂和取余；首先我们要知道私钥(n,d)此时的密文为c
首先进行求幂c^d;然后取余(c^d)%n;此时的(c^d)%n就是我们的明文m了